Digital Signal Processing with Machine Learning: The Fourier Series

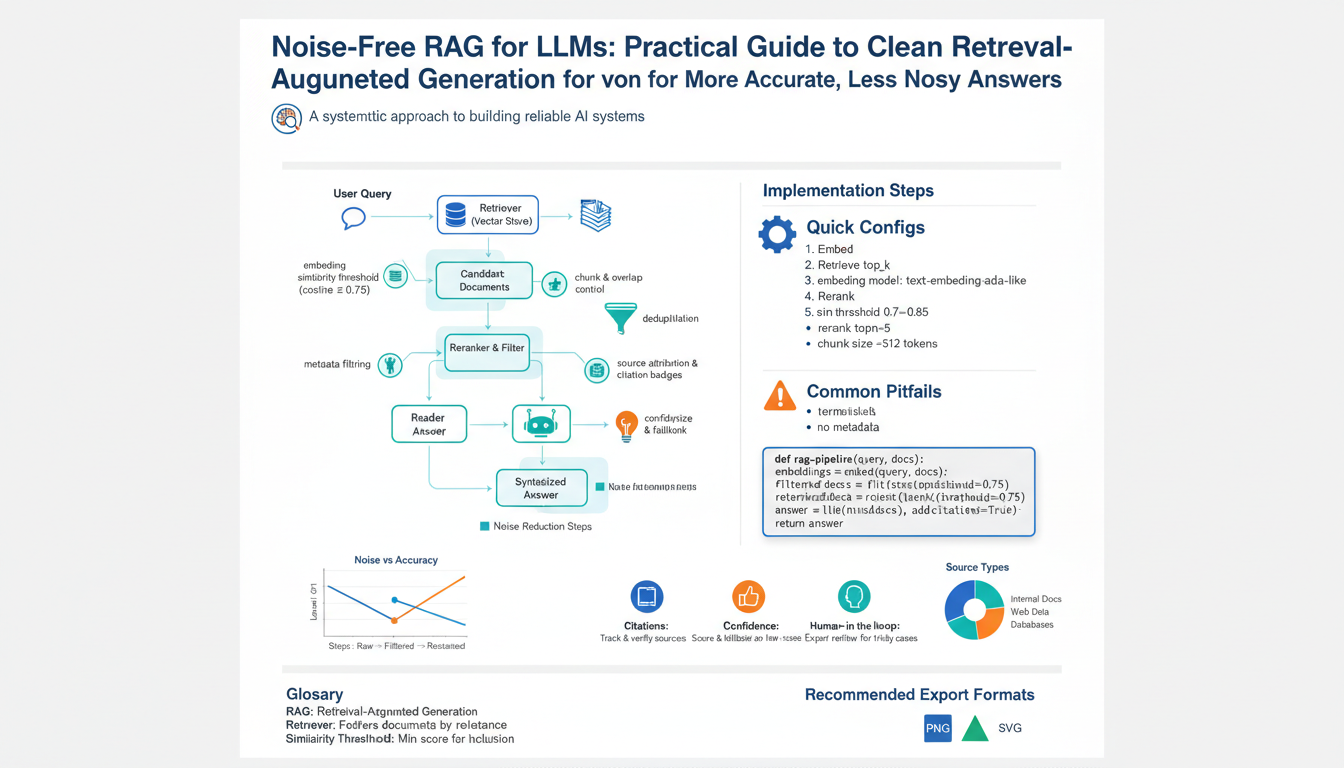
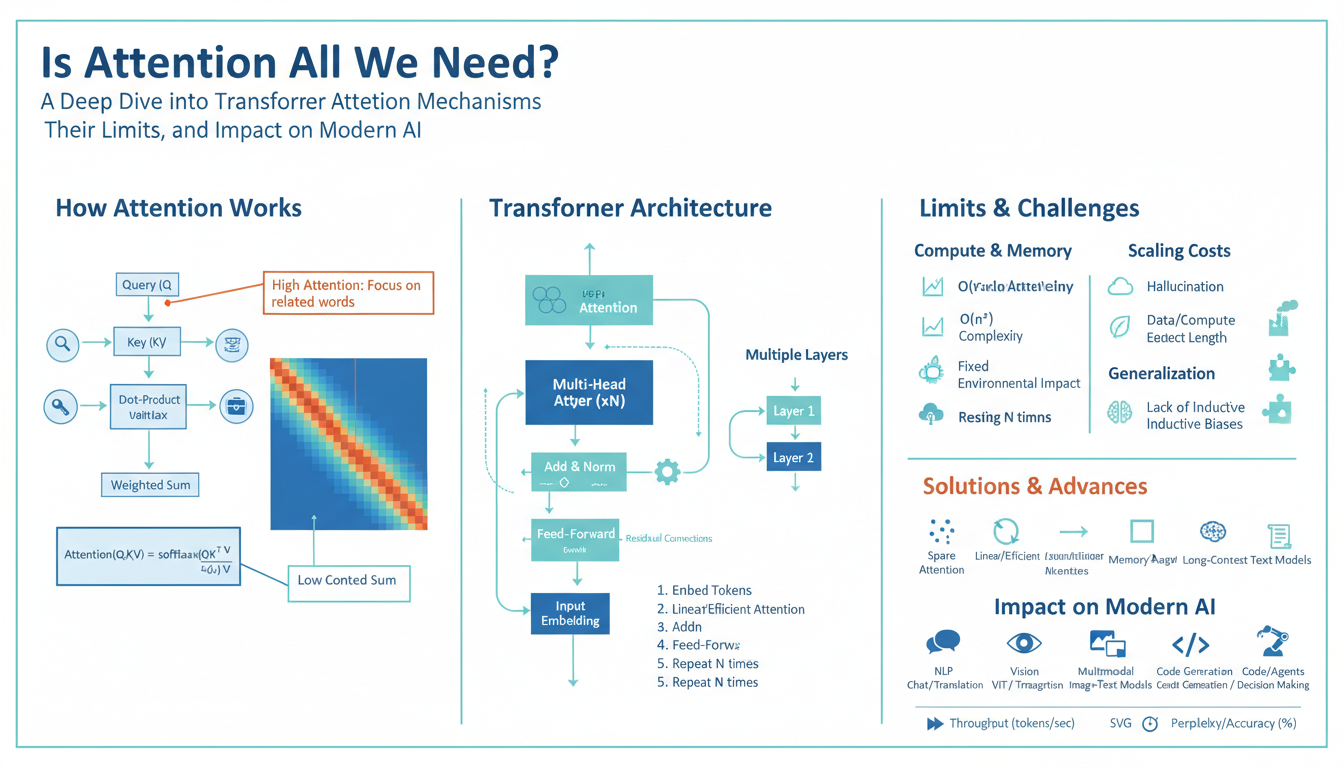
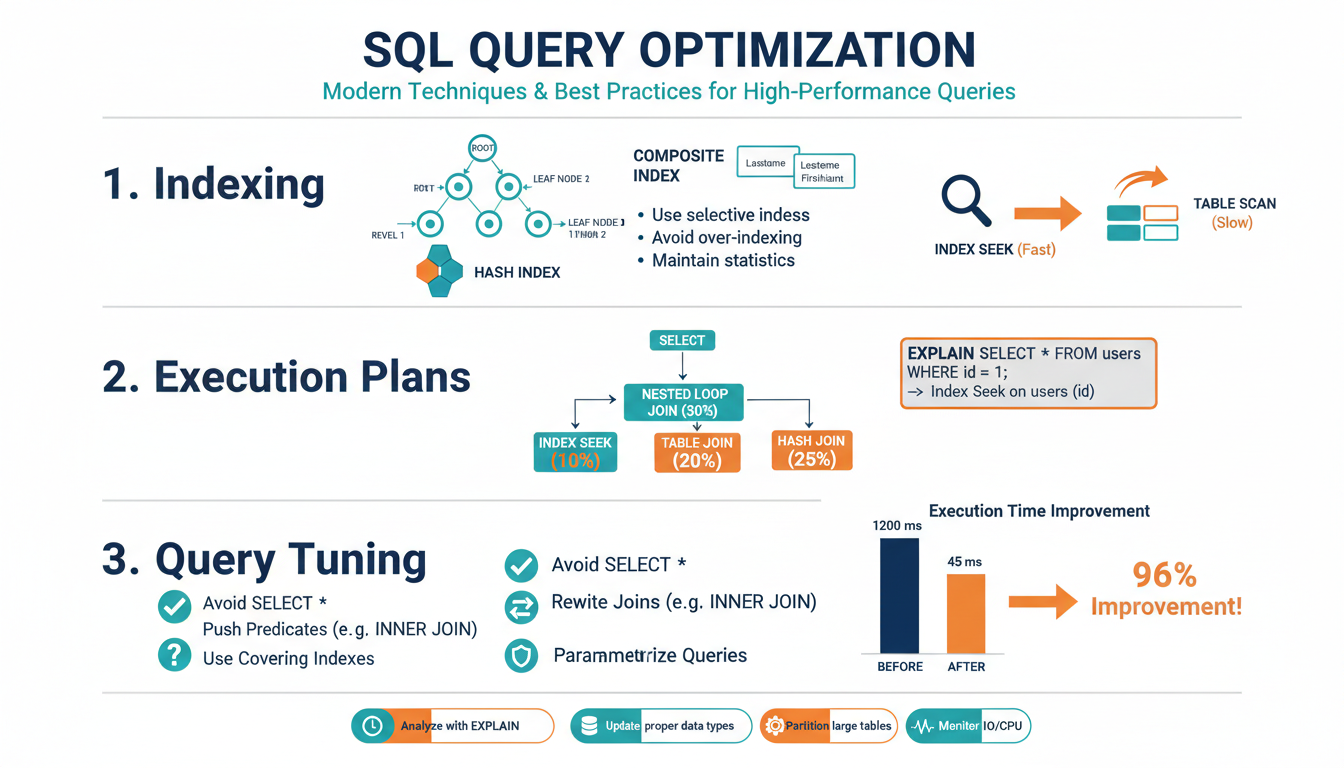
Introduction to Digital Signal Processing (DSP)

Digital Signal Processing (DSP) is a foundational discipline that underpins countless modern technologies, from mobile communications to medical imaging and multimedia entertainment. At its core, DSP is concerned with the analysis, manipulation, and interpretation of signals—streams of data that often represent real-world phenomena such as audio, images, sensor readings, or even financial trends. The goal is to extract useful information, enhance signal quality, or prepare data for further analysis, storage, or transmission.

In the digital age, most signals are digitized for processing—converted from their natural analog form into a sequence of discrete numbers. This digital transformation unlocks powerful methods that are not only more robust to noise but also more flexible and efficient in implementation via computers or specialized hardware. Digital processors can precisely apply mathematical operations that would be challenging or even impossible in the analog domain.

The history of DSP is closely linked with the rise of computing power in the 20th century. Once limited by the speed and cost of computers, DSP now enables real-time applications thanks to advances in integrated circuits and efficient algorithms. Some common examples include:

• Audio enhancement in smartphones or music apps, where noise is reduced and sound quality is boosted.
• Image processing in cameras and medical scanners, such as MRI or CT, to sharpen images or highlight specific structures.
• Wireless communications, including Wi-Fi and 5G, relying on DSP to encode, decode, and correct signals sent through noisy environments.

DSP works through a series of well-defined steps:

1. Sampling: Capture the analog signal at regular intervals to create a discrete-time representation. The sampling theorem states that the sample rate must be at least twice the highest frequency in the signal to accurately reconstruct it.
2. Quantization: Map the sampled values to finite levels, introducing some error that DSP techniques aim to minimize or correct.
3. Processing: Apply mathematical operations (such as filtering, transforming, or compressing) to extract information or enhance the signal as needed.
4. Reconstruction: In some applications, convert the digital signal back to analog form for playback, transmission, or actuation.

Understanding these processes is crucial for anyone exploring the intersection of DSP and machine learning. As machine learning models increasingly rely on rich data inputs—such as spoken commands, sensor feeds, or images—the ability to preprocess and optimize these signals using DSP techniques ensures improved accuracy and efficiency. For deeper technical dives into DSP basics, resources like this beginner’s DSP tutorial from EE Times provide practical walkthroughs and code examples.

The Role of Machine Learning in Modern DSP

Machine learning (ML) is revolutionizing digital signal processing (DSP) by introducing smarter, adaptive techniques for analyzing complex data. Traditionally, DSP relied heavily on mathematical frameworks like the Fourier series to break down signals into sinusoidal components. However, the explosion of real-world data—from audio signals in smartphones to image processing in medical devices—presents challenges that classic methods alone cannot address.

In particular, ML enhances DSP by offering the ability to recognize intricate patterns and features within signals that may be hidden or nonlinear. This is especially valuable for signals with noise, distortion, or those that change over time. For example, recent studies have demonstrated that neural networks can outperform traditional Fourier-based techniques in denoising or reconstructing signals.

How Machine Learning Augments DSP:

• Feature Extraction: Instead of manually designing filters or features, ML algorithms can automatically discover optimal representations of a signal. For instance, convolutional neural networks (CNNs) can learn time-frequency features similar to those found via the Fourier series, but are more adaptable to nuances in different datasets. This ability to learn feature hierarchies improves the accuracy and interpretability of signal processing tasks.
• Nonlinear Relationships: Many real-world signals exhibit nonlinear behavior—which traditional linear transforms like the Fourier series cannot fully capture. ML models, especially deep learning architectures, are excellent at learning these nonlinearities. This leads to improved performance in tasks like speech recognition, where background noise or speaker variation can pose substantial hurdles for classic methods.
• Automation and Adaptation: Modern DSP applications demand fast adaptation to new environments. For example, in wireless communications, signals may be influenced by dynamic interference or channel conditions. ML models can be trained on real-time data to continuously update and adapt their processing strategies, as detailed by IEEE research in adaptive filtering.

Examples of ML in DSP:

• Speech Enhancement: Deep learning is widely used to enhance speech quality by filtering out noise that would not be effectively removed by conventional Fourier-based filters. You can see a deep dive into these techniques at Nature Digital Medicine.
• Medical Signal Analysis: In electrocardiogram (ECG) analysis, ML algorithms detect patterns indicative of disease, going beyond what simple frequency analysis can achieve. For further reading, refer to the American Heart Association’s review on AI in cardiac care.

In summary, machine learning is more than just an add-on to digital signal processing; it is driving a fundamental shift in how engineers and scientists approach complex signals. By integrating ML with classic DSP tools like the Fourier series, practitioners can tackle problems that were previously infeasible, paving the way for smarter, more adaptive technology across countless applications.

Understanding the Fourier Series: Fundamentals and Applications

The Fourier series is a fundamental tool in both signal processing and the broader field of applied mathematics. At its core, the Fourier series decomposes complex, periodic signals into a sum of simple, sinusoidal components. This technique, developed by Joseph Fourier in the early 19th century, forms the basis for many modern applications in engineering, physics, and even machine learning.

What is the Fourier Series?

The Fourier series enables us to express any periodic function as an infinite sum of sines and cosines. More formally, if you have a function f(x) that is periodic on an interval, its Fourier series representation is:

f(x) = a_0 + \sum_{n=1}^{\infty} \left[ a_n \cos(nx) + b_n \sin(nx) \right]

Here, a₀, aₙ, and bₙ are called the Fourier coefficients, which quantify the contribution of each harmonic (sine or cosine) to the overall signal. The computation of these coefficients involves integration over one period of the function, encapsulating the core mathematical principles underpinning signal decomposition.

How the Fourier Series Works

1. Periodicity: The process begins with a periodic signal—whether it be an electrical signal, sound wave, or any repeating pattern. This property is essential for the mathematical validity of the Fourier series.
2. Sinusoidal Decomposition: By projecting the signal onto sine and cosine functions of varying frequencies, the Fourier series isolates distinct frequency components. Imagine breaking down a musical chord into its individual notes—each note corresponds to a sine or cosine term.
3. Reconstruction: The resulting sum of sinusoids, each scaled by the appropriate coefficients, reconstructs the original signal with remarkable fidelity. As more terms are included, the approximation improves and converges to the original function.

Key Applications of the Fourier Series

The versatility of the Fourier series lies in its wide range of applications:

• Signal Processing: It underpins much of filter design and spectral analysis, enabling engineers to analyze and manipulate the frequency content of signals for communications and audio processing.
• Machine Learning: In machine learning, particularly in domains like time-series analysis, Fourier transforms facilitate feature extraction and dimensionality reduction, improving model performance and interpretability. Discover more in this detailed CMU lecture note on DSP for ML.
• Image Compression: Methods like JPEG utilize the mathematical principles of Fourier analysis to compress images efficiently by representing image content in terms of its frequency components. More can be learned through the discrete cosine transform, a variant closely related to the Fourier approach.

Examples of Practical Implementation

• Audio Signal Analysis: Consider a recorded piece of music. Using the Fourier series, you can break it down into constituent pitches, identify dominant notes, and even design filters that enhance or suppress specific sounds.
• Stock Market Data: In analytics, Fourier decomposition reveals periodic trends within noisy financial data, aiding in forecasting and anomaly detection.
• Biomedical Engineering: Electrocardiogram (ECG) signals can be analyzed through Fourier analysis to filter out noise and highlight meaningful rhythms in a patient’s heartbeat, as explained by the National Institutes of Health.

The Fourier series bridges the gap between the time domain and the frequency domain, providing a language for understanding complex, repetitive phenomena. Mastery of this tool unlocks new possibilities for innovation in signal processing, machine learning, and beyond.

Why the Fourier Series is Crucial for Machine Learning Tasks in DSP

The Fourier Series is a mathematical cornerstone in the realm of digital signal processing (DSP), and its implications are profound for machine learning practitioners. Understanding why it is so vital requires delving into both the nature of signals and how modern learning algorithms leverage signal information extracted in the frequency domain.

1. Unpacking Signal Representation

At the core, signals—whether audio, sensor data, or even some image streams—are often represented as time-domain sequences. Many real-world signals have underlying patterns that are hard to discern in this raw time-based format. The Fourier Series provides a way to express these signals as sums of simple sinusoids (sines and cosines), each corresponding to specific frequencies. This transformation is crucial because many hidden patterns or features are much easier to spot or extract when observed in the frequency domain. For those seeking a deeper mathematical treatment of this mechanism, ScienceDirect offers a comprehensive overview of the Fourier Series.

2. Feature Extraction and Engineering in Machine Learning

Modern machine learning tasks, like audio classification, speech recognition, and even anomaly detection, often require robust features. The Fourier Series enables engineers to transform raw waveforms into their frequency components. For instance, a speech signal can be decomposed so that different phonemes become distinguishable thanks to their unique frequency signatures. This process is critical in preprocessing workflows for tasks ranging from music genre analysis to predictive maintenance in industrial IoT. To see Fourier transformations in action for ML, consider Google’s practical guide on audio preprocessing.

3. Noise Reduction and Signal Enhancement

Real-world signals are riddled with noise that can mislead machine learning models. By applying the Fourier Series, it’s possible to localize noise in certain frequencies and selectively suppress them, leading to cleaner inputs for model training. For example, medical diagnostics using ECG or EEG sensors benefit immensely from such denoising techniques, which can improve the performance of classification algorithms further downstream. The National Center for Biotechnology Information outlines studies demonstrating the effectiveness of Fourier-based denoising in biomedical applications.

4. Interpretability and Model Transparency

When machine learning decisions are based on interpretable frequency-domain features, it becomes easier to understand why a model acts as it does—such as identifying which frequency bands are most relevant for a prediction. This transparency is particularly valued in high-stakes fields like finance and healthcare, where model explainability is paramount. For a broader discussion of explainable AI in signal processing, Nature Machine Intelligence provides an accessible overview.

5. Enabling Advanced Architectures

Finally, the Fourier Series underpins techniques like the Fast Fourier Transform (FFT), which are not just preprocessing tools but also integrated into the architectures of cutting-edge machine learning models, including certain neural networks for time-series data. FFT’s computational efficiency allows real-time signal processing crucial in applications like streaming analytics and AI-powered IoT. A foundational perspective on this evolution can be found at Coursera’s course on FFT in machine learning.

In summary, the Fourier Series is indispensable for machine learning in DSP not only for feature extraction and noise reduction but also for model transparency and computational efficiency. Its contributions elevate the accuracy, interpretability, and speed of modern AI solutions built for the world of signals.

Key Techniques: Feature Extraction Using the Fourier Series

Feature extraction is a pivotal stage in many machine learning and signal processing workflows. One of the most celebrated mathematical tools used for this purpose is the Fourier Series. By decomposing signals into their constituent frequencies, the Fourier Series unveils patterns and relationships that may be obscured in the original data, empowering machine learning algorithms to make more accurate predictions and classifications.

Why Use the Fourier Series for Feature Extraction?

Traditional signals—such as audio, sensor, or time-series data—are often complex and high-dimensional. The Fourier Series allows us to interpret these signals in terms of their frequency components, enabling us to highlight features that are robust to noise, invariant to certain transformations, and more interpretable for training algorithms. For a deep dive into the mathematics behind the Fourier Series, you can consult the Wolfram MathWorld.

Steps to Extract Features Using the Fourier Series

1. Signal Preprocessing:
   • Begin by cleaning your data—this involves tasks such as normalization, detrending, and removing artifacts that may skew the Fourier coefficients.
   • For practical guidance, check out scientific papers on preprocessing for time-series analysis.
2. Apply the Fourier Transform:
   • Transform your signal from the time domain to the frequency domain using the Discrete Fourier Transform (DFT) or its computationally efficient cousin, the Fast Fourier Transform (FFT). For periodic signals, the Fourier Series expansion is equivalent to these discrete transforms in finite intervals.
   • Learn more about FFT and its implementation at Khan Academy.
3. Identify Key Frequency Components:
   • Extract the magnitudes and phases of the main harmonics, which represent features such as dominant pitches in audio or repetitive cycles in sensor data.
   • For instance, in ECG signal analysis, certain frequencies are correlated with medical conditions; thus, isolating these components leads to informative features (see this clinical review).
4. Feature Selection and Reduction:
   • Due to the high dimensionality of frequency data, it can be beneficial to select only the most significant coefficients or to aggregate related frequencies using statistical descriptors (e.g., energy, entropy). This reduces complexity and improves model performance.
   • For further reading on dimensionality reduction in frequency-based features, see scikit-learn’s official guide.
5. Integration Into Machine Learning Pipelines:
   • The selected Fourier features become input variables for classifiers, regressors, or clustering algorithms. In audio classification, for example, these frequency features form the backbone of voice recognition systems.
   • For real-world applications, refer to the detailed case studies in O’Reilly’s Python Machine Learning.

Examples of Fourier-Based Feature Extraction

Let’s walk through two practical use cases:

• Music Genre Classification: Audio tracks are split into short frames, and the Fourier Transform is computed for each. The spectral centroid and dominant frequency bands are extracted, enabling the classifier to distinguish genres based on rhythmic and harmonic content.
• Wearable Sensor Activity Recognition: The Fourier coefficients highlight walking, running, and resting cycles from accelerometer data. These frequency-domain features are then used by machine learning models to predict user activity.

Feature extraction with the Fourier Series not only reveals hidden data structures but also improves the interpretability and efficiency of machine learning algorithms. For a comprehensive overview of digital signal processing in conjunction with machine learning, consider reviewing the Springer textbook on Signal Processing for Machine Learning.

Real-World Examples: Machine Learning Models Powered by Fourier Analysis

Fourier analysis sits at the heart of digital signal processing (DSP)—and, increasingly, it is being leveraged by cutting-edge machine learning (ML) models to unlock new possibilities. Let’s explore how Fourier analysis is powering real-world ML solutions across various sectors, detailing the mechanisms and impact of integrating these powerful mathematical tools.

Speech Recognition Systems

Modern voice-activated assistants such as Siri and Google Assistant rely on transforming sound waves into a format suitable for machine learning algorithms. The raw audio is first broken into small frames, and the Discrete Fourier Transform (DFT) is applied to convert time-domain data into frequency-domain features. This transformation allows ML models to more effectively recognize subtle patterns in human speech—such as different accents, intonations, and background noises.

• Step 1: Audio sample is collected and pre-processed (e.g., noise reduction).
• Step 2: Each frame undergoes DFT or its fast implementation, FFT (Fast Fourier Transform) to extract frequency components.
• Step 3: Resulting spectral features are fed into neural networks, such as Recurrent Neural Networks (RNNs) or transformers, for classification.

This approach has led to robust voice recognition engines capable of operating in complex, real-world environments.

Image Compression and Enhancement

Many popular image compression formats—like JPEG—employ a form of Fourier analysis known as the Discrete Cosine Transform (DCT), which is closely related to the Fourier Series. When combined with machine learning, this frequency-based representation aids in automated image enhancement and artifact removal.

• Step 1: The image is divided into small blocks (e.g., 8×8 pixels).
• Step 2: DCT is applied to each block, converting pixel data into frequency coefficients.
• Step 3: ML algorithms, such as convolutional neural networks (CNNs), process these coefficients for denoising or super-resolution tasks.

Professional research, such as in the paper Image Super-Resolution Using Deep Convolutional Networks, demonstrates how frequency-domain processing, aided by ML, dramatically increases output quality for medical imaging, satellite data, and more.

Emotion and Music Analysis

Many ML applications in musicology and emotion detection use the Fourier Series to break down audio into meaningful features. In music, the frequency spectrum reveals the tonal structure—essential for tasks like genre classification or automatic chord recognition. In sentiment analysis, emotional cues can often be tied to certain frequency patterns and rhythms.

• Step 1: Audio signals are decomposed into frequency bands via Short-Time Fourier Transform (STFT).
• Step 2: Spectral features—such as pitch, timbre, and rhythm—are extracted to form input vectors for ML models.
• Step 3: Models such as logistic regression or deep learning architectures classify the emotional intent or musical style.

This synergy between DSP and ML is reshaping industries. For example, the Magenta project by Google showcases how neural networks compose or analyze music using Fourier-based spectral features.

Anomaly Detection in Healthcare Monitoring

Continuous monitoring of heart signals (ECG) or brain waves (EEG) often uses Fourier analysis to extract patterns from the time series data. By feeding frequency domain data into advanced ML classifiers, healthcare professionals can detect anomalies—such as arrhythmias or epileptic seizures—far more reliably.

• Step 1: Physiological signals are collected and digitized for analysis.
• Step 2: Fourier Transform reveals dominant and abnormal frequency components.
• Step 3: Trained ML models, such as Random Forests or Support Vector Machines (SVMs), classify or predict health events in real time.

This process is instrumental in building smart, real-time healthcare solutions that improve patient outcomes and reduce response times in critical situations.

Whether it’s enhancing human-computer interaction, transforming multimedia content, or saving lives in medical settings, the marriage of Fourier analysis and machine learning is enabling new breakthroughs. The ongoing research and innovation highlighted by IEEE and academic institutions reinforce just how pivotal these combined technologies are for the future of digital signal processing.