Cross Validation in Machine Learning: Unlocking the Secret to Smarter Model Building

Introduction to Cross-Validation in Machine Learning

In the realm of machine learning, building robust and reliable models often involves much more than just fitting a dataset to a chosen algorithm. The real challenge lies in ensuring that a model performs well not only on the training data but also on unseen data. This is where cross-validation emerges as an essential tool, helping machine learning practitioners build models with superior generalization capabilities.

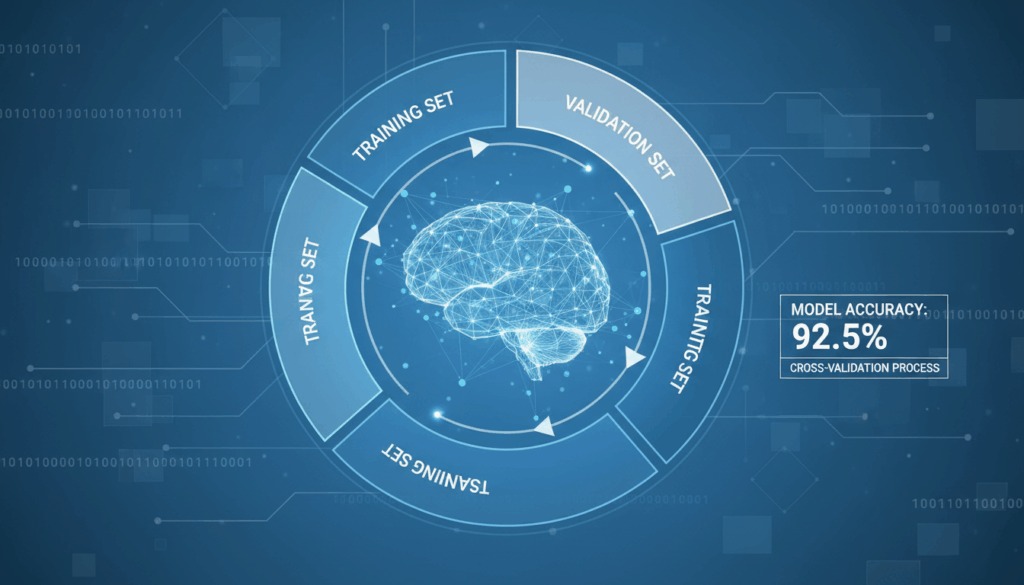
Cross-validation is a statistical technique used to evaluate the performance of a model by partitioning the data into subsets, training the model on some subsets while validating it on others. This iterative process helps overcome issues related to overfitting—a situation where a model learns the training data too well, including its noise and outliers, and performs poorly on new data.

The most basic form of cross-validation is k-fold cross-validation. Here, the dataset is divided into k equally sized folds or partitions. The model is trained k times, each time using a different fold as the validation set while the remaining folds form the training set. For instance, if k=5, the data is divided into five parts. In the first iteration, the first fold is used for validation, and the rest for training. This process repeats until each fold has served as the validation set once. The performance metric (such as accuracy, precision, or recall) is averaged over all k trials, providing a more accurate assessment of the model’s ability to generalize.

Another popular variant is stratified k-fold cross-validation. This approach is particularly useful when dealing with imbalanced datasets, where certain classes or outcomes are more frequent than others. Stratification ensures that each fold is a good representative of the whole, maintaining the same class proportion as the entire dataset.

Yet another method is leave-one-out cross-validation (LOOCV), which is an extreme case of k-fold cross-validation where k equals the number of data points in the set. Here, the model is trained on all data points except one and validated on the remaining one. While LOOCV can provide a thorough evaluation, it is computationally expensive and typically used for small datasets.

The application of cross-validation extends beyond model selection to hyperparameter tuning, where it helps in finding the optimal set of parameters for an algorithm. Techniques like grid search and random search leverage cross-validation to evaluate different model configurations.

By employing cross-validation, one can mitigate the risk of overfitting, assure better generalization, and ultimately enhance the trustworthiness of the predictive model. This technique thus lays the foundation for improving the reliability and performance of machine learning applications across various domains.

Understanding the Need for Cross-Validation

Cross-validation is a pivotal concept in machine learning due to its integral role in ensuring model reliability and generalization. As straightforward as training a model might seem, the complexity of handling data variability and model tuning necessitates robust evaluation techniques. Cross-validation steps in to bridge this gap, addressing several critical issues inherent in model development.

One of the fundamental challenges in machine learning is the risk of overfitting. Overfitting occurs when a model learns the training data, including its noise and anomalies, too well. This results in high accuracy on the training set but poor performance on new, unseen data. Cross-validation helps mitigate this risk by providing a structured way to assess how the results of a statistical analysis will generalize to an independent dataset. Through repeated training and testing on different dataset partitions, practitioners gain a real-world approximation of model performance.

Another key reason for using cross-validation is the preliminary nature of training datasets. Often, datasets don’t perfectly represent the problem’s domain or might not be sufficiently large or uniform. By dividing data into multiple subsets for iterative training and validation, cross-validation provides insights into the model’s consistency across varied segments of data, thereby promoting a more robust evaluation methodology.

Cross-validation is instrumental in hyperparameter tuning. Machine learning models have parameters that need to be set before the training process—these are called hyperparameters. Examples include the learning rate for neural networks or the number of neighbors in a K-Nearest Neighbors (KNN) model. Selecting optimal hyperparameters is crucial for model performance, and cross-validation aids in this by testing various combinations across different data splits, offering empirical evidence to guide parameter adjustments.

Moreover, cross-validation supports model selection in environments where multiple algorithms might be suitable for a given task. For instance, when deciding between linear regression and decision trees, cross-validation can be employed to evaluate which model performs better under a consistent testing framework. It quantifies performance consistency, thus enabling informed decisions about the best algorithm to deploy in production.

In domains where data imbalance is prevalent, the need for cross-validation becomes even more pronounced. Data imbalance, where certain classes dominate the dataset, can skew performance metrics in straightforward train-test splits. Cross-validation techniques, such as stratified k-fold, ensure that each split maintains the distribution of classes, thereby providing an unbiased evaluation.

The overarching aim of cross-validation, therefore, is to ensure that the model’s deployment into real-world scenarios will meet expectations. By simulating how the model will perform on unseen data during the testing phase, practitioners are better equipped to make decisions that ensure long-term success and reliability. In sum, cross-validation is not just a technique; it is a foundational practice in the machine learning workflow that facilitates intelligent model design and evaluation. Its adoption leads to the creation of models that are not only accurate but also robust and adaptable to varied data circumstances.

Types of Cross-Validation Techniques

Cross-validation in machine learning is pivotal for ensuring model robustness and performance. Various techniques can be adopted depending on the dataset size, computational resources, and specific model considerations.

k-Fold Cross-Validation

One of the most common cross-validation methods is k-fold cross-validation. Here, the data is partitioned into k subsets or “folds.” The model is then trained k times, each time using a different fold as the validation set while the remaining folds are used for training. For instance, with k=5, the dataset is divided into five parts. The model is trained using four of these parts, with the remaining part used for testing. This is repeated five times, with each fold serving as the test set once. The performance metrics obtained from these iterations are averaged to provide a comprehensive performance evaluation of the model.

An important facet of k-fold cross-validation is selecting an appropriate k value. A common choice is k=10, providing a balance between computational efficiency and a reliable estimate of model performance. Smaller k values may lead to high variance, while larger values reduce bias but increase computational cost.

Stratified k-Fold Cross-Validation

Stratified k-fold cross-validation is a variant of k-fold that ensures each fold has a representative distribution of classes, particularly useful for imbalanced datasets. By maintaining the distribution of the target variable, stratified sampling prevents overfitting to specific data distributions found only in certain folds.

For example, in a binary classification problem where one class vastly outnumbers the other, stratified k-fold ensures that each fold mirrors the overall distribution, ensuring each subset is a mini-representation of the entire dataset.

Leave-One-Out Cross-Validation (LOOCV)

In LOOCV, a more extreme form of cross-validation, the number of folds is equal to the number of data points. Each observation is used once as a validation set, with the remaining data points serving as the training set. This method is highly thorough but computationally expensive, often utilized for very small datasets. While it provides an intense evaluation, it may not always be practical due to its demanding resources.

Leave-p-Out Cross-Validation

An extension of LOOCV, leave-p-out cross-validation involves setting aside p data points as the validation set, training the model on the remaining dataset. This technique can provide more meaningful insights when p is chosen thoughtfully, though it requires substantial computing time and is generally limited to smaller datasets.

Time Series Cross-Validation

In time-dependent datasets, where the sequence of data points is crucial, standard cross-validation strategies might not be suitable. Time series cross-validation, or “rolling” cross-validation, is specifically designed to handle these types of datasets. Typically, the model is trained on a growing set of sequential data points and tested on the subsequent step, respecting the order of time. This technique ensures that historical data is used to predict future events, mimicking real-world scenarios where future events cannot influence past decisions.

Suppose a dataset tracks stock prices. Using time series cross-validation, a model might be trained on price data from January to March and tested on April data, ensuring that time-consistent decisions are made.

Monte Carlo Cross-Validation (Shuffle-Split)

Unlike traditional k-fold cross-validation that deterministically splits datasets, Monte Carlo cross-validation randomly shuffles and splits the data into training and testing sets multiple times. After each split, the model is evaluated and the results are averaged. This method offers flexibility in the size of training and test sets and the number of iterations, providing insights into model variance and flexibility across different data configurations.

In conclusion, the choice of cross-validation technique significantly affects model evaluation, and selecting the appropriate form is crucial for the task at hand. Understanding the strengths and constraints of each method allows for more accurate and efficient model performance insights, ultimately guiding better decision-making in machine learning projects.

Implementing K-Fold Cross-Validation in Python

To effectively implement k-fold cross-validation in Python, you begin by preparing the necessary packages and datasets. Python, with its rich ecosystem of libraries, provides the tools needed to efficiently carry out this task. The scikit-learn library is particularly well-suited for this, as it includes built-in methods for cross-validation.

Start by importing relevant libraries:

import numpy as np
from sklearn.model_selection import KFold
from sklearn.datasets import load_iris
from sklearn.linear_model import LogisticRegression

Load and Prepare Data

For this implementation, consider a well-known dataset, such as the Iris dataset, to simplify the demonstration. This dataset is available through scikit-learn:

data = load_iris()
X = data.data
y = data.target

Initialize K-Fold Cross-Validation

Decide on the number of folds (k). Common practice suggests 5 or 10 folds, but this can be adjusted based on the dataset size and computational resources:

k = 5  # number of folds
kf = KFold(n_splits=k, shuffle=True, random_state=42)

Here, shuffle=True shuffles the dataset before splitting, ensuring a random distribution, and random_state ensures reproducibility.

Conduct Cross-Validation

Initialize a loop that iterates over each training/validation split:

model = LogisticRegression(max_iter=200)
scores = []

for train_index, test_index in kf.split(X):
    X_train, X_test = X[train_index], X[test_index]
    y_train, y_test = y[train_index], y[test_index]

    # Train the model
    model.fit(X_train, y_train)

    # Evaluate the model
    score = model.score(X_test, y_test)
    scores.append(score)

average_score = np.mean(scores)
print(f'Average accuracy: {average_score:.2f}')

Explanation of the Process

Model Initialization: Logistic Regression is chosen for its simplicity and interpretability in multiclass classification.
Training and Testing: For each fold, the model is trained using the training subset and evaluated on the validation subset.
Record Performance: The accuracy from each fold is stored and averaged at the end to provide a robust estimate of model performance.

Interpretation of Results

The average accuracy across the folds gives an estimate of how the model is expected to perform on unseen data. This process helps detect issues like overfitting that might not be apparent from a single split of the data.

Further Enhancements

Hyperparameter Tuning: Incorporate hyperparameter tuning with techniques such as GridSearchCV together with k-fold to find the best model configuration.
Stratified Variants: In cases of unbalanced datasets, you can use StratifiedKFold to ensure each fold maintains the class distribution.

Implementing k-fold cross-validation in Python using scikit-learn provides a robust framework to improve and validate machine learning models, ensuring adaptability and reliability in practical applications.

Advantages and Limitations of Cross-Validation Methods

Cross-validation plays a critical role in model evaluation within machine learning, offering a systematic way to assess how a model will perform on an independent dataset. However, like any method, cross-validation has its advantages and limitations that one must consider during its application.

Cross-validation’s primary advantage is its ability to provide a more accurate estimate of a model’s performance compared to a simple train-test split. By repeatedly partitioning the dataset into distinct training and validation subsets and averaging the results, cross-validation minimizes biases associated with random data splits. This helps ensure that observed performance metrics are more likely to reflect the model’s behavior on unseen data.

Advantages

Reduction in Overfitting Risk: One key strength is its efficacy in reducing the tendency of a model to overfit on a single dataset. By evaluating the model on different subsets of data, cross-validation provides insight into its generalizability beyond the initial sample.
Better Use of Data: Cross-validation makes efficient use of the available data. Since multiple subsets are used for validation, it maximizes the input data for training the model in each iteration, leading to potentially better-trained models compared to conventional methods.
Robust Performance Metrics: A notable advantage is the provision of a more comprehensive view of a model’s performance. Metrics obtained from cross-validation, such as average accuracy or F1-score, reflect a reliable performance estimate across different data splits.
Parameter Tuning and Model Selection: By assisting in hyperparameter tweaking and model selection processes, cross-validation supports finding an optimal configuration or model. Multiple configurations can be evaluated systematically to discern which performs best consistently, facilitating informed decisions.

Limitations

Increased Computational Cost: One of the significant downsides of cross-validation is its computational intensity. Running multiple training and validation cycles increases the computational load, especially in scenarios involving large datasets or complex models.
Time Consumption: Closely related to computational cost, the process of cross-validation can be time-intensive. This can be a limiting factor in environments where rapid iteration and turnaround are necessary, such as in time-sensitive projects or limited-resource scenarios.
Sensitive to Data Shuffling: Though cross-validation’s random partitioning helps mitigate biases, it can still be sensitive to data shuffling processes, particularly when dealing with datasets having dependencies or structured patterns that are disrupted by shuffling.
Limited Suitability for Time-Series Data: Conventional cross-validation techniques, like k-fold, are not ideally suited for time-series datasets due to the temporal dependencies of the data. Specialized methods, such as time-series cross-validation, must be employed to respect the chronological order, adding complexity to its application.
Potential for Variance in Results: Although averaging results from multiple folds offers a stable performance indication, variance can sometimes occur due to different partition compositions, especially in datasets where every instance carries significant information due to limited data size.

To maximize the benefits of cross-validation while mitigating its drawbacks, practitioners often complement its standard application with insights from exploratory data analysis, domain knowledge, and computational optimizations to strike a balance between evaluation depth and resource expenditure. By doing so, they ensure that cross-validation remains a valuable component in the model development toolkit. It enhances the reliability and robustness of machine learning models poised for real-world deployment.