Transformer Origins and Attention Basics
Researchers shifted away from recurrent and strictly convolutional sequence models when they needed faster training and better handling of long-range dependencies. The breakthrough replaced recurrence with a mechanism that lets every token directly attend to every other token in a sequence, enabling full pairwise interaction and wide parallelism during training.
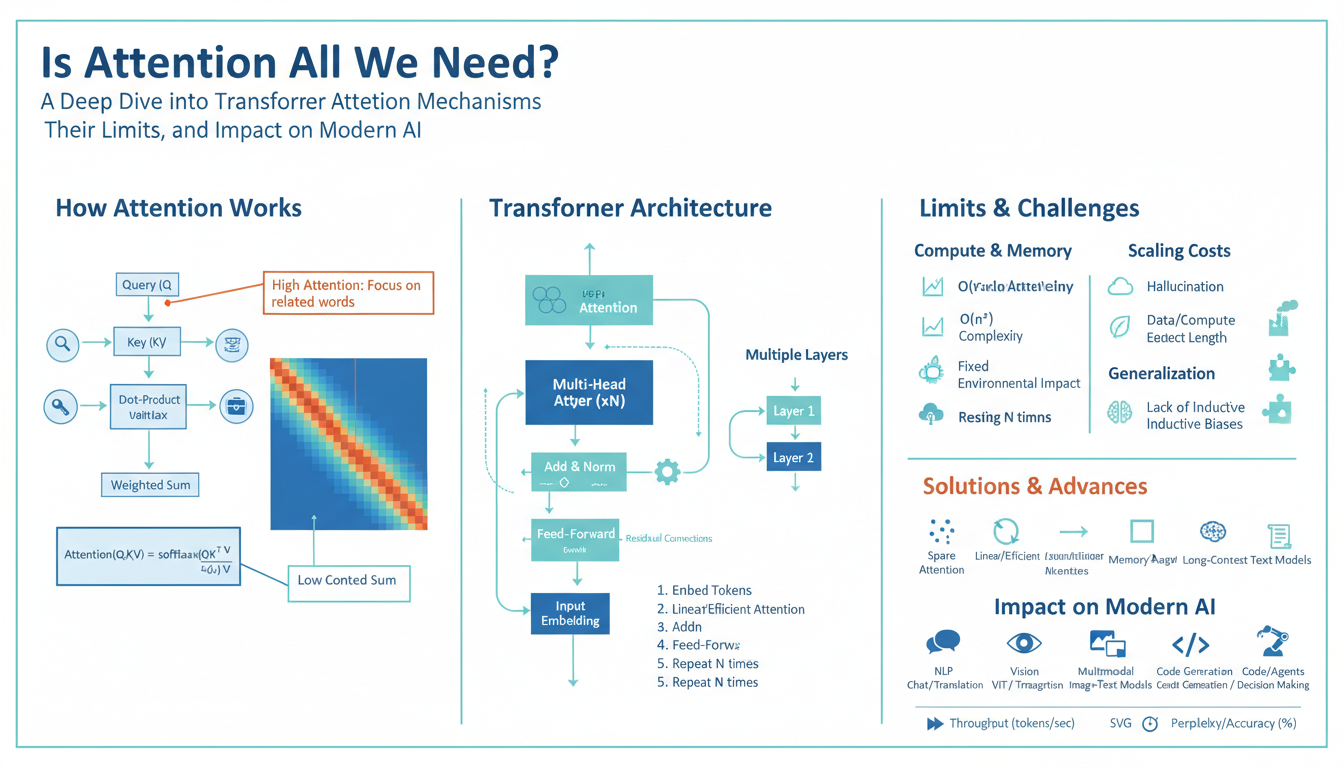
At the core is self-attention: each input token is projected into three vectors—query (Q), key (K), and value (V). Compatibility scores are computed as the scaled dot product between queries and keys; a softmax turns those scores into attention weights, which are used to produce a weighted sum of values. Compactly: Attention(Q,K,V)=softmax(QK^T/√d_k) V. This single formula captures how the model routes information across positions and dynamically focuses on relevant context.
Multi-head attention runs several attention operations in parallel on different linear projections, letting the model capture diverse relationships (syntax, coreference, positional cues) simultaneously. Because attention is position-agnostic, positional encodings (learned or sinusoidal) are added so the model can reason about token order.
Architecturally, layers stack multi-head self-attention, feed-forward subnetworks, residual connections, and normalization. In encoder–decoder setups the decoder uses masked self-attention plus cross-attention to encoder outputs for generation. The result is a performant, scalable building block that underpins modern large language models by offering efficient parallelism and strong long-range context modeling.
How Scaled Dot-Product Attention Works
Each token is linearly projected into query (Q), key (K) and value (V) vectors. Attention computes pairwise compatibilities by taking dot products between queries and keys to form a score matrix: S = Q K^T. To avoid extremely large logits as vector dimensionality grows, each score is scaled by 1/√d_k (where d_k is the key dimension): S' = S / √d_k. A row-wise softmax converts these scaled scores into attention weights that sum to one for each query, and the final output for each query is the weighted sum of values: Attention(Q,K,V) = softmax(QK^T / √d_k) V.
Scaling prevents softmax from saturating (very peaky distributions) when d_k is large, stabilizing gradients and improving training. Practically, for sequence length n and model dim d, QK^T is an n×n matrix (O(n^2 d) time and O(n^2) memory), so attention gives full pairwise interactions but at quadratic cost. Masking is applied before softmax for autoregressive decoders or padding tokens. Multi-head attention runs several independent scaled dot-product attentions with smaller d_k in parallel, letting different heads focus on different relations before a final linear recombination.
Multi-Head Attention Intuition and Role
Think of multiple heads as parallel “lenses” that view the same sequence through different linear projections so the model can learn diverse relational patterns at once. Each head computes attention on its own projected queries, keys and values (e.g., head_i: Q_i,K_i,V_i), producing outputs that are concatenated and linearly recombined into the layer output. This lets one head focus on short-range syntactic ties (modifier→noun), another on long-range coreference, another on positional cues or punctuation, and so on, rather than forcing a single attention map to represent every relationship simultaneously.
Concretely, running h smaller attentions preserves overall model dimensionality while giving capacity to specialize: Attention_i = softmax(Q_i K_i^T / √d_k) V_i, Output = Concat(head_1…head_h) W^O. Specialization improves expressiveness and helps training because distinct subspaces can develop complementary features without interfering with each other’s gradients.
In practice this yields richer, more interpretable interaction patterns (some heads consistently capture syntax, others copy or aggregate key tokens). There are trade-offs: beyond a point extra heads give diminishing returns and can be redundant, so h and per-head dimension are tunable hyperparameters. The key practical takeaway is that multi-head parallelism provides a compact, efficient way for transformers to represent multiple simultaneous relations in a sequence, enabling the model to route different types of contextual information through separate pathways.
Limitations: Scaling, Complexity, And Biases
Attention gives transformers powerful, general-purpose routing, but it has clear practical limits. Naive self-attention costs O(n^2) memory and O(n^2·d) compute for sequence length n, so very long contexts quickly become infeasible on current hardware; this drives workarounds like chunking, sliding windows, and sparse or low-rank attention approximations, each trading fidelity for tractability. At large scale, model size and depth amplify engineering complexity: training becomes sensitive to optimization hyperparameters, communication overhead across accelerators rises, and many attention heads or layers can be redundant or brittle—making interpretation and debugging harder.
Architectural fixes (sparse attention, linearized kernels, local+global hybrids, retrieval augmentation, mixture-of-experts) reduce cost but add implementation, tuning, and distributional complexity. They introduce new failure modes: approximations can miss rare long-range dependencies, retrieval systems depend on index quality, and conditional compute can create unstable gradients or brittle capacity allocation. Latency, energy use, and deployment constraints remain first-order concerns for real-world systems.
Biases are another core limitation: attention maps reflect learned correlations, not causation. Models trained on large web corpora inherit social, cultural, and label biases; attention can amplify spurious signals (e.g., over-attending to demographic proxies) and reproduce harmful stereotypes. Mitigation requires active data auditing, targeted fine-tuning, adversarial and counterfactual testing, calibration, and human-in-the-loop review. Simple fixes like more data or larger models do not eliminate these risks and can make them harder to detect.
Practical takeaway: balance capacity with efficient approximations, invest in tooling for interpretability and distributed training, and treat bias mitigation as an ongoing engineering requirement rather than a one-time step.
Alternatives and Improvements to Attention
Researchers and engineers mitigate attention’s quadratic cost and brittleness through two complementary directions: cheaper approximations and alternative sequence operators. Algorithmic approximations replace full dense attention with sparse or low-rank computations—examples include locality windows plus selected global tokens, sparse attention patterns, kernelized “linear” attention that factors softmax into streaming kernels, and Nyström-style low-rank solves—each reduces memory/compute at the expense of exact pairwise fidelity. Architecturally, hybrids and replacements introduce different inductive biases: structured state-space models (SSMs) capture very long-range dynamics with near-linear cost; recurrence or convolutional blocks reintroduce local compositionality and efficient streaming; memory-augmented layers and retrieval-augmented modules externalize context to an index instead of attending to everything in-line; and conditional compute (MoE) scales capacity without uniformly increasing cost. Other practical improvements keep attention but make it more robust or efficient: relative and rotary positional encodings restore order sensitivity; head pruning, attention dropout variants, and sparsity regularization reduce redundancy; cross-layer parameter sharing and pre-norm setups stabilize deep training; and adapter/prompt tuning plus retrieval make fine-tuning cheaper while improving factuality. Each choice trades expressiveness, implementation complexity, and failure modes—approximate attention can miss rare long-range dependencies, external retrieval depends on index quality, and MoE introduces routing instability. In practice, designers combine techniques: local+global attention for medium-length contexts, memory or retrieval for ultra-long context, and SSM or linearized kernels where streaming and low latency matter. The right mix depends on sequence length, latency/energy budget, and the need for faithful long-range interactions versus scalable throughput.
Attention’s Impact on Modern AI
Attention redefined how models route and integrate information across a sequence: by allowing every token to weigh every other token, it enabled massive parallelism during training, reliable handling of long-range dependencies, and compact mechanisms (like multi-heads) that let models represent many relation types simultaneously. That shift underpins modern pretrained systems—from masked encoders to large autoregressive generators—by making dense context aggregation and scalable transfer learning practical.
Practically, attention paved the way for powerful emergent behaviors: effective fine-tuning and prompt-based control, robust cross-modal fusion, few‑shot and in‑context learning, and straightforward conditioning via cross‑attention or retrieval. Multi‑head patterns also supply useful interpretability signals (some heads specialize to syntax, coreference, copying), helping diagnostics and targeted interventions during model development.
Those benefits come with tradeoffs that shape deployment and ongoing research. Dense attention’s O(n^2) memory and compute drives work on sparse, low‑rank, and kernelized approximations, retrieval‑augmented pipelines, structured state‑space blocks, and conditional compute to hit latency and energy targets. Attention maps can mirror spurious correlations from data, so mitigation (data curation, targeted fine‑tuning, adversarial tests) remains essential. In short, attention is the functional core of many modern AI capabilities, while its limitations continue to steer architectural innovation and engineering practice.