Why train/test split matter: A statistical perspective

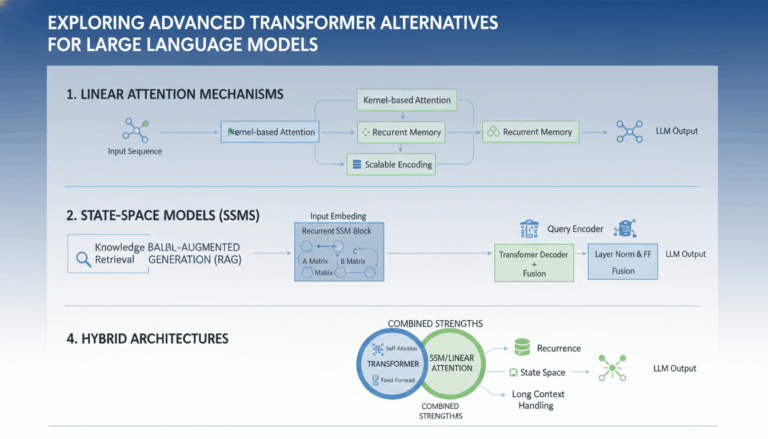
Understanding the Basics: What is Train/Test Split?

At the core of building any predictive model in machine learning lies the concept of the train/test split. Imagine you have a collection of data—this could be anything from housing prices to clinical patient records. To evaluate how well your model might perform on new, unseen data, it’s essential to divide your dataset into two separate subsets: a training set and a test set.

The training set is the portion of data used to “teach” your model about patterns, relationships, and structures. Algorithms learn from this subset, adjusting their internal parameters based on the examples and outcomes available in the training data. The test set, on the other hand, is reserved strictly for evaluation. By keeping this data separate, we can assess how well the model generalizes to unseen data, mimicking real-world scenarios where future predictions must be made on data it hasn’t encountered before.

This separation is crucial for avoiding a common pitfall called overfitting. Overfitting occurs when a model performs exceptionally well on the training data but fails to deliver accurate predictions on new datasets. Essentially, it “memorizes” the training examples rather than learning generalizable patterns. For more on this subject, consider referencing the tutorial from scikit-learn, a widely respected Python machine learning library that offers in-depth guidance on data splitting and validation.

The process of performing a train/test split usually involves the following steps:

Randomization: Randomly shuffle the dataset to ensure that both the train and test sets are representative samples of the whole. This step minimizes bias that could arise from ordered data.
Splitting: Allocate a defined portion (often 70-80%) to training, and the remainder (usually 20-30%) to testing. For complex datasets or high-stakes applications, additional splits like a validation set or techniques like cross-validation may also be used.
Ensuring Independence: Guarantee that no data point appears in both the training and test set, maintaining the integrity and independence of the evaluation process.

For practical examples, you can explore the detailed walkthroughs and case studies provided by Machine Learning Mastery, which demonstrate how to implement train/test splits using real-world datasets.

Understanding the basics of train/test splitting is a foundational step for anyone aiming to build reliable, unbiased, and robust predictive models. It ensures that when you deploy your model, you can trust its predictions are not just tailored to the data you’ve already seen, but are predictive and useful for future, unseen cases.

The Role of Train/Test Split in Model Evaluation

Imagine training a predictive model on historical data and then immediately asking it to predict the same examples it just saw. It would likely perform exceptionally well—but would it be truly capable of handling unseen, real-world scenarios? This is precisely where the importance of a train/test split comes in, offering a statistically sound way to evaluate how a machine learning model will perform on new, previously unseen data.

At its core, splitting your data into a training set and a testing set is about preventing “overfitting,” a common pitfall where a model becomes too tailored to the quirks of the training data and fails to generalize. When we evaluate models only on the data they were trained on, we risk significantly overestimating their accuracy and utility. The simple act of withholding a portion of the data for unbiased evaluation mirrors real-world scenarios more faithfully and provides a clearer measure of the model’s robustness.

Let’s break down how this split works and why it’s statistically crucial:

Creating the Split: Typically, data is partitioned—often 70/30 or 80/20—where the larger portion is used for training and the smaller for testing. This allocation allows most data to be used for learning structures and patterns, while the remainder is reserved for a realistic evaluation. More advanced variations include cross-validation and stratified sampling, especially when dealing with imbalanced datasets (see sampling techniques in R).
Model Development and Tuning: The training set is used for everything involved in building the model: fitting, parameter estimation, and sometimes, even hyperparameter tuning through cross-validation. This process ensures that the model learns from the majority of data it will be allowed to “see.”
Objective Evaluation: Once trained, the model is tested against the reserved data. Its performance metrics—accuracy, precision, recall, F1-score—gauged on the test set directly reflect its expected future performance. This division simulates deployment, where new data will not have labels available for feedback, reinforcing the role of validation in credible research (see Google’s ML Crash Course).
Generalization and Statistical Validity: The train/test split iterates the principle of generalization error, a foundational concept in statistics and machine learning. Evaluating on unseen data helps estimate how the model’s predictive power might hold up in real-world settings. Models evaluated only on training data tend to provide overly optimistic insights, which may not translate outside the initial sample (for further reading, see Machine Learning Mastery).
Practical Example: Suppose you’re building a model to predict if a patient has a disease based on lab results. If you train and evaluate on the same data, you risk providing false assurance that your model is highly accurate. By properly splitting, you gain confidence that your model’s performance is not just a fluke of the sample, but a reliable estimation for patients outside your dataset.

Ultimately, the role of the train/test split in model evaluation is not just a technicality, but a statistical imperative. It echoes decades of best practices for ensuring that scientific findings are replicable and honest. For a deep dive on responsible evaluation, visit the Google Developers Machine Learning Course on Validating Data.

Common Pitfalls Without Proper Data Splitting

Neglecting to properly split data into training and testing sets is a surprisingly common mistake—one that can undermine the integrity of your entire analytical workflow. As tempting as it may be to train and evaluate a model on the full dataset, doing so risks significant statistical pitfalls. Let’s delve into the common consequences and why they matter for anyone seeking reliable results.

1. Overfitting: The “Too-Good-To-Be-True” Trap

When you allow a model access to the entire dataset for both training and evaluation, it can easily “memorize” the answers. This phenomenon, known as overfitting, means your model will likely achieve near-perfect performance—on the data it’s already seen. But when exposed to new data, its performance can plummet. Overfitting erodes the generalizability of your model, rendering your insights untrustworthy in real-world applications. For detailed examples of overfitting and why train/test split mitigates it, see this Machine Learning Mastery guide.

2. Data Leakage: Unintentional Peeking

Without a proper train/test split, information from outside the training dataset can inadvertently influence the model. This problem, known as data leakage, artificially inflates a model’s performance and can happen in subtle ways, such as when data preprocessing steps are performed before splitting. For example, normalizing the entire dataset before splitting means the test set’s statistical properties are already known to the training process. Data leakage is a critical issue discussed in-depth by Coursera’s Data Science courses.

3. Statistical Bias: The Mirage of High Metrics

If you evaluate a model on training data, you bias your performance metrics, such as accuracy, precision, or recall. In reality, these numbers reflect how well the model fits peculiarities in your particular dataset—not its ability to generalize. Without a separate test set, you lack a credible estimate of how your model will fare on unseen data. As Towards Data Science elaborates, failing to split data subjects your analysis to misleading conclusions that may not replicate in production or in future research.

4. Unrealistic Model Selection and Hyperparameter Tuning

Often, analysts tune hyperparameters to achieve the best results. If the same dataset is used for both training and testing, this process becomes circular, simply finding settings that best exploit peculiar quirks in the data rather than seeking truly robust solutions. This issue is amplified with complex models and large hyperparameter spaces. Academic resources such as Scikit-learn’s documentation on cross-validation detail how proper splitting guards against this issue and preserves model integrity.

5. Reproducibility and Scientific Integrity

In both academia and industry, reproducibility is crucial. When results are obtained with improper data splitting, they cannot be reliably replicated—even minor dataset changes might drastically shift outcomes. Properly partitioned train/test sets provide a foundation for robust, credible insights that others can validate.

Real-World Example: Housing Price Prediction

Imagine building a model to predict housing prices and evaluating it on the same data you trained on. Your model boasts a sky-high R² score. You deploy it, only to find that it performs poorly for new, incoming listings. Here, improper data split led to misleading confidence in your model’s predictive capability, emphasizing why train/test split is a data science best practice. For more on implementing correct splits in practice, see guidance from Google’s Machine Learning Crash Course.

In summary, failing to split your data appropriately invites a host of analytic errors, undermining not just model metrics but the very conclusions drawn from data. By recognizing and avoiding these pitfalls, you can harness the true power of statistical analysis and machine learning.

How Data Leakage Skews Model Performance

Data leakage occurs when information from outside the training dataset is used to create the model, resulting in overly optimistic performance estimates that won’t hold up in real-world scenarios. This often happens when the distinction between training and test datasets is blurred or ignored, undermining the reliability of model evaluation.

Imagine a scenario where a machine learning model is developed to predict whether a loan applicant will default. If any feature in the training dataset contains information that would only be available after the loan is approved—such as repayment behavior—using this feature constitutes data leakage. The model appears to perform exceptionally well on both the training and test sets. However, once deployed, it fails to generalize because it was trained on information unavailable at the time of decision-making, rendering performance metrics misleading.

Let’s break down the steps of how this can happen:

Data Preparation Overlap: For example, if you normalize the dataset before splitting it into training and test sets, you inadvertently allow the test set to influence the training set’s parameters. This is why normalization should always be performed after splitting the data (source).
Incorrect Target Variable Inclusion: Sometimes, derived variables created from the target variable (such as profit margin post-purchase in a sales prediction task) are mistakenly included as predictors. When these variables leak into the training process, the model memorizes rather than learns underlying patterns.
Temporal Leakage: If time plays a role in your data (think stock market prediction), failing to respect chronological order when splitting data can result in the model peeking into the future. Models trained this way are not suitable for real-time predictions, and actual performance quickly drops (NIH – Data leakage in machine learning).

The dangers of data leakage are particularly pronounced in high-stakes fields like healthcare or finance, where faulty predictions can have serious consequences. For instance, a notable real-world example involved a pneumonia risk prediction model that performed extremely well in tests—until it was discovered that factors only available after a diagnosis had leaked into the dataset, rendering results spurious in actual use.

Mitigating data leakage requires vigilance. Always split your data into training and test sets before any data transformation, feature generation, or model selection. Review the features for signals or proxies that could inadvertently carry target information. Adopting rigorous cross-validation and understanding the domain context are essential components of any sound data science workflow (Scikit-learn – data leakage).

Taking care to avoid data leakage not only maintains the integrity of performance evaluation, but also ensures that your model delivers accurate, actionable insights when deployed in the real world.

Train/Test Split vs. Cross-Validation: Key Differences

Choosing the right method for evaluating machine learning models is crucial, as it directly impacts the accuracy and reliability of your results. The train/test split and cross-validation are two widely used strategies for this purpose, but it’s important to understand how they differ and when you might prefer one over the other.

Train/Test Split:

The train/test split is a straightforward approach in which the dataset is divided into two groups: training data and testing data. Typically, a common ratio like 70/30 or 80/20 is used. The model is trained on the training data and then evaluated on the testing set. This method is fast and easy to implement, making it popular for large datasets or quick experiments.

Steps:
1. Randomly shuffle the dataset to reduce bias.
2. Divide the data into a training set (e.g., 80%) and a test set (e.g., 20%).
3. Fit the model using the training data.
4. Evaluate the model’s performance with the test set to estimate real-world performance.
Example: In image recognition, you might use 10,000 labeled images, train your model on 8,000, and then assess its ability to label the remaining 2,000.

However, the simplicity of the train/test split comes with a potential risk: high variance in performance estimation. If the test set does not represent the overall dataset well (i.e., it is not a good statistical sample), your model might appear to perform better or worse than it actually does in practice. For more details, see this Machine Learning Mastery article.

Cross-Validation:

Cross-validation, particularly k-fold cross-validation, offers a more robust alternative. Here, the dataset is divided into k equally sized subsamples, or “folds.” The model is trained and validated k times, each time using a different fold as the test set and the others as the training set. The final performance metric is then averaged across all folds.

Steps:
1. Shuffle and split the dataset into k folds (commonly 5 or 10).
2. For each fold:
  - Train the model on k-1 folds.
  - Test the model on the remaining fold.
3. Repeat the process k times so each fold serves as the test set once.
4. Calculate the average performance score across all folds.
Example: With a 5-fold cross-validation on 1,000 data points, you train and evaluate your model five times: each time, 800 data points are used for training and 200 for validation, rotating which partition serves as the validation set.

This approach provides a lower variance estimate of your model’s skill, making it particularly valuable for smaller datasets where a single train/test split could produce misleading results. By repeatedly training and testing the model, cross-validation ensures that every observation is used for both training and testing, leading to a more reliable estimate of out-of-sample performance. Read more about the theory and advantages of cross-validation at scikit-learn’s documentation and this IBM overview.

Key Differences:

Bias-Variance Trade-off: Train/test split has higher variance but is less biased towards subsets of data. Cross-validation reduces variance by averaging results, providing a more stable estimate of model performance.
Computational Cost: Train/test split requires only one model training, while cross-validation trains k models, making it more computationally intensive.
Suitability: For very large datasets, a train/test split is often sufficient. For limited data and for model selection or hyperparameter tuning, cross-validation is recommended.

Understanding these distinctions is essential for anyone aiming to build predictive models that perform well not just on paper, but in the real world. Method selection can mean the difference between a mirage of accuracy and genuine, reproducible results.

Statistical Bias and Variance: The Impact of Improper Splitting

When we build machine learning models, how we split our data between training and testing sets has a profound impact on the reliability and accuracy of our results. One crucial area where improper data splitting can lead to serious problems is in the statistical properties of bias and variance.

Bias refers to errors introduced by approximating a real-world problem, which might be complex, by a much simpler model. When a dataset is not properly split, such as by accidentally including similar or identical records in both the training and test sets, the model may learn patterns that are not truly representative of new, unseen data. This is known as data leakage, and it artificially lowers measured bias, creating the illusion of a better-performing model. To understand data leakage and its impact, check out this detailed overview from Machine Learning Mastery.

On the other hand, variance measures how much model predictions change if we use a different slice of the dataset for training. If we don’t ensure that the train and test sets are statistically representative and mutually exclusive, we get misleading variance estimates. High variance means your model is likely overfitted—performing well on the training data but poorly on unseen examples. For a comprehensive explanation, scikit-learn’s documentation covers the concept with practical code examples.

Why does this matter? Consider the following concrete scenario:

A medical researcher trains a model to predict disease outcome, but uses overlapping patient records in both training and testing sets. The model achieves 98% accuracy; however, upon deployment, its real-world performance drops drastically. This was caused by biased evaluation due to improper splitting.
Alternatively, suppose a data scientist randomly splits a highly time-dependent stock market dataset, breaking the chronological order. The model’s variance seems low, but in the real world, its performance is unstable because it did not encounter the true temporal patterns during training or testing.

To minimize bias and variance due to splitting issues, practitioners often use techniques such as cross-validation, and stratified sampling. These methods help ensure that the statistics of the training set mirror those of the test set and reflect the dataset’s true distribution. For more, see the discussion on best practices by University of Toronto’s Geoffrey Hinton.

Ultimately, rigorous train/test splitting isn’t just a technical detail; it’s a safeguard against misleading conclusions, equipping data scientists with results that are robust, replicable, and meaningful in real applications.

Overfitting and Underfitting: The Split Factor

In the world of machine learning, overfitting and underfitting are common pitfalls that can undermine the predictive power of a model. Central to managing both of these issues is the decision to split data into distinct training and testing sets. But why does this split matter so much, and how does it directly impact the balance between overfitting and underfitting?

Overfitting occurs when a model learns not only the underlying patterns in the training data, but also the noise—those quirks and idiosyncrasies that don’t generalize beyond the sample. This is akin to memorizing exam answers rather than understanding the material. When a model is overfitted, it performs exceptionally well on the training data but fails to deliver accurate predictions on new, unseen data—a clear sign the model’s knowledge is superficial and too narrowly tailored.

Conversely, underfitting happens when a model is too simplistic, capturing neither patterns nor noise. Imagine a student who only read the textbook overview before the exam; the answers are often wrong because the understanding is too shallow. An underfitted model produces poor results on both the training and testing sets, signaling a need for more complexity or better feature selection.

This is where the concept of the train/test split becomes vital:

Detection of Overfitting: By intentionally setting aside a portion of data for testing, we create an opportunity to assess how well the model generalizes. A model that performs well on training data but poorly on test data indicates overfitting. This diagnostic step can’t be achieved if all data is used solely for training. For more on this, the statistics department at Stanford University provides an in-depth treatment in their classic textbook “The Elements of Statistical Learning.”
Guarding Against Underfitting: By monitoring performance on both splits, data scientists can detect when a model’s assumptions are too restrictive. If test and train performance are equally poor, the problem likely lies in an underfitted model. In such cases, more sophisticated algorithms or additional features might be required. Consider exploring the Scikit-learn documentation for practical techniques to address underfitting through smarter feature engineering and model selection.

Practical Example:

Suppose you are building a regression model to predict house prices. If you use the entire dataset for training, your model might learn to associate certain house IDs with high prices—a meaningless correlation in the real world. By splitting your data, you challenge the model to prove itself on houses it has never “seen” before. If it passes, you can be confident the model has learned something meaningful about real estate pricing, not just dataset quirks. This helps you avoid both the traps of overfitting (by testing generalizability) and underfitting (by tracking improvements as you iterate model design).

Ultimately, the train/test split acts as a safeguard, ensuring the model’s insights are robust and transferable. For a statistical deep-dive, check out this Harvard Data Science Review article on the science of train/test splits, which includes valuable insights on their optimal use in modern data analysis.

Best Practices for Train/Test Splitting in Machine Learning

Successful machine learning relies not just on powerful algorithms, but fundamentally on how we prepare and partition our data. The seemingly minor decision of how to split the dataset into training and testing sets can have profound effects on model accuracy, reliability, and real-world performance. Here, we delve into the best practices for executing this step with statistical rigor and practical awareness.

Ensure Statistical Independence

When creating train/test splits, one of the primary goals is to guarantee statistical independence between the two sets. If data points in the test set are too similar to those in the training set, the model’s performance metrics become artificially inflated, leading to data leakage. For example, in time series forecasting, always split chronologically — not randomly — to prevent the model from “seeing the future.” Always ask: Can information from one set bleed into the other? If so, adjust your splitting strategy accordingly.

Stratified Splitting for Balanced Representation

Imbalances within your dataset — such as skewed class distributions in classification tasks — can undermine your model’s evaluation. Use stratified splitting to ensure the train and test sets reflect the same proportions of each class. This is critical for datasets with rare events or underrepresented classes. Most modern libraries like scikit-learn provide tools for stratified sampling, which helps maintain statistical representativeness and avoids misleading metrics like inflated accuracy from dominant classes.

Randomness and Reproducibility

Randomized splitting mitigates the risk of bias from inadvertently structuring the split. Always use a random_state or equivalent seed to ensure that results are reproducible. Reproducibility is essential, especially in research and regulated industries, where you may need to justify or rerun experiments. Document the exact random seed and methodology to foster transparency and trust in your results.

Choosing the Right Split Ratio

The most common ratios for train/test splits are 80/20, 70/30, or 60/40, depending on dataset size. With larger datasets, you can reserve a smaller portion for testing while still capturing sufficient variation. For smaller datasets, apply alternatives such as k-fold cross-validation to maximize the utility of precious samples and obtain a more robust estimate of model performance. Adjust the split conservatively if your application has high stakes, such as in healthcare or finance, to avoid overfitting or underestimating model risk.

Avoiding Data Snooping

Feature engineering, scaling, and imputation should be performed strictly within the confines of the training data. Applying preprocessing steps using the full dataset introduces data snooping bias, as knowledge from the test set can influence your model, corrupting the validity of evaluation metrics. Ensure all preprocessing pipelines are fit on the training set and then applied to the test set independently.

Practical Example: Train/Test Split in Python

from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(
    X, y, test_size=0.2, random_state=42, stratify=y
)

In this example, stratify=y ensures that class proportions are preserved in both sets, random_state=42 guarantees reproducibility, and test_size=0.2 allocates 20% of data for testing.

Adhering to these best practices not only provides more robust models but also upholds the standards of statistical integrity and scientific credibility in your machine learning projects.

Case Studies: Real-World Consequences of Incorrect Splits

In practice, improper handling of the train/test split can have far-reaching implications. Here, we’ll explore a few real-world case studies to illustrate the magnitude of these consequences and highlight why meticulous splitting is critical for credible results.

Medical Diagnostics: The Peril of Data Leakage

One of the most notable examples comes from the field of medical diagnostics, where a model trained to detect diseases can inadvertently learn from information that belongs strictly to the test set. For example, in a landmark study on breast cancer detection, data leakage occurred when images from the same patient appeared in both training and test sets. This overlap resulted in overly optimistic performance estimates because the model was, in effect, tested on data it had already seen. When the test set was properly segregated, accuracy dropped significantly, revealing the true performance of the model (Nature Medicine).

Step 1: Data from all patients should be uniquely partitioned to avoid overlap between training and test sets.
Step 2: Ensure any cross-validation respects grouping by patient to prevent indirect leakage.
Example: Without proper split, a promising cancer-detecting AI system was found to be less effective and unreliable when tested on new, previously unseen patients.

Financial Forecasting: Overfitting and False Confidence

Financial institutions rely heavily on predictive analytics to make lending decisions or forecast stock prices. A famous case involved a model that predicted stock prices, but the test split was not independent of training data. Instead, the random selection resulted in temporal leakage, where past data was mixed with future data, ultimately inflating the expected accuracy. Once corrected to ensure strict temporal separation, the model’s performance regressed to the mean (ScienceDirect).

Step 1: Split data according to time, keeping historical data in the training set and future data in the test set.
Step 2: Re-evaluate model metrics to ensure forecasting validity under real-world conditions.
Example: A model that looked successful in simulation failed in deployment, costing the firm both money and trust.

Retail and Recommendation Systems: Sampling Bias and Generalization

E-commerce platforms often use recommender systems to suggest products. A well-documented failure arose when the test split was done such that only popular users’ data ended up in both train and test sets. This was not representative of the broader user base. The system performed exceptionally well during evaluation but failed among new or less active users post-launch (ACM Digital Library).

Step 1: Analyze user demographics/behavior before splitting, ensuring diversity and representativeness in both sets.
Step 2: Regularly update evaluation methodologies to align with changing user behavior and business goals.
Example: Despite stellar initial evaluation, the recommendation system led to subpar personalization and user disengagement after rollout.

These cases highlight that errors in train/test split aren’t just academic. They lead to misleading metrics, costly business mistakes, and can ultimately compromise public trust. Read more about best practices for data splitting and bias prevention at Google’s ML Guide.